摩尔-库伦公式
摩尔-库伦公式
摩尔-库伦公式是岩石力学中描述岩石剪切强度的经典公式。该公式表示了岩石的剪切强度与岩石的正应力状态之间的关系。
1776年法国科学家库伦(C.A.Coulomb)总结土的破坏现象和影响因素,提出土的破坏公式为:
根据砂土试验结果得到:
τf=σn* tan(φ)
对于粘性土,可给出更为普遍的表达式:
τf= c +σn * tan(φ)
摩尔(Mohr)继续库伦的早期研究工作,提出材料的破坏是剪切破坏的理论,认为在破裂面上,法向应力与抗剪强度之间存在着函数关系,即:
τf=f(σ)
其中,τ表示岩石的剪切强度,c表示岩石的凝聚力(cohesive strength)(即在正应力为零时的剪切强度),σn 表示岩石正应力的法向分量,φ表示岩石的内摩擦角(angle of internal friction)。内聚力代表了材料颗粒之间的吸引力或粘结力,它使得材料具有一定的内聚性。内聚力越大,材料越难破坏。内摩擦角代表了材料颗粒之间的摩擦阻力,它决定了材料在受到切应力时的抵抗能力。内摩擦角越大,材料越能抵御切应力,具有更高的强度。
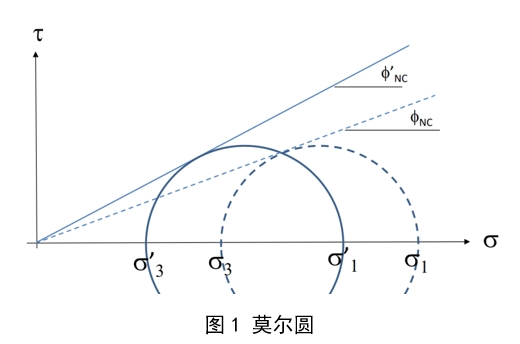
摩尔-库伦准则的图示可以用一个正应力-切应力的图形来表示,这个图形被称为莫尔圆。在二维平面上,莫尔圆由一条直线和一个围绕该直线旋转的圆所组成。直线代表了法向应力的变化,圆代表了切应力的变化。通过绘制莫尔圆,可以确定材料的强度状态和破坏条件。
当应力状态达到摩尔-库伦屈服准则的破坏条件时,材料将发生破坏。根据该准则,破坏发生的判据如下:
1.当切应力达到极限强度时,即 τ = c + σn * tan(φ),材料将开始发生破坏。
2.在莫尔圆上,当切应力达到最大值时,即位于莫尔圆的最右侧点,材料将发生全面破坏。
理论介绍
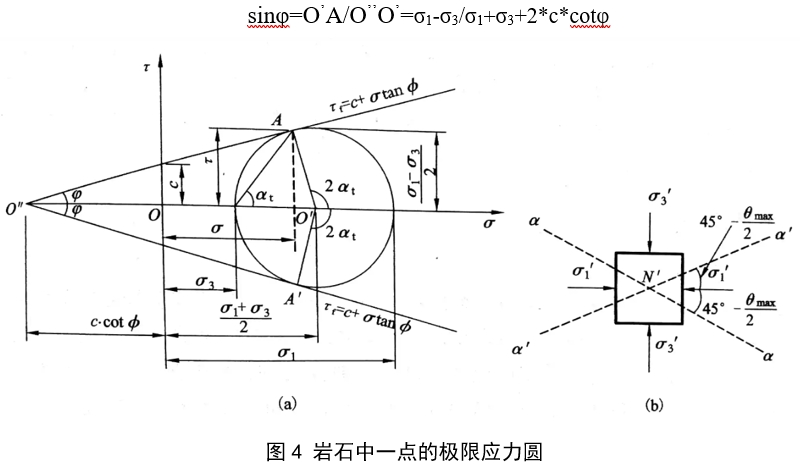
当岩石中任一平面上的某点剪应力等于岩石的抗剪强度时,该点即处于濒于破坏的临界状态,此临界状态即称为"极限平衡状态”。该状态下各种应力之间的关系称为"极限平衡条件”。
由“应力分布”可求得在自重和竖向附加应力作用下任一点M的应力状态σ1和σ3 [图2(a)]。为简单起见,以平面应变课题为例,研究该点是否产生破坏。如图2(b)所示,该点单元体两个相互垂直的面上分别作用着最大主应力σ1和最小主应力σ3。若忽略其自身重力,则根据静力平衡条件,可求得任一截面m-n上的法向应力σ和剪应力τ为
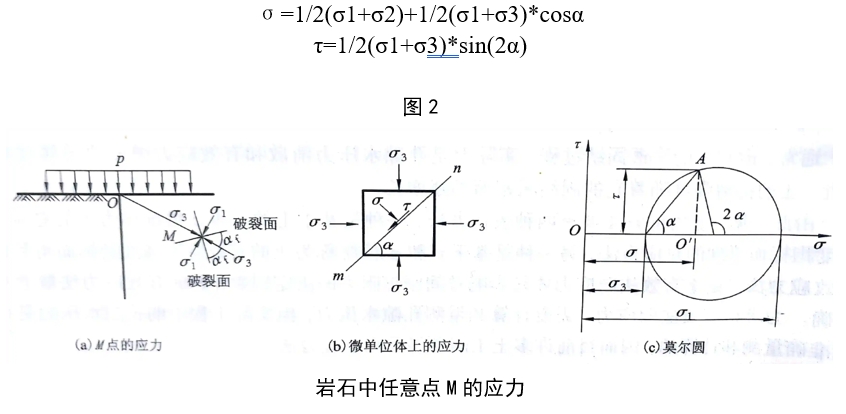
由材料力学应力状态分析可知,以上σ,τ与σ1,σ3的关系也可用摩尔-应力圆表示[图2(c)]。其圆各点的坐标即表示该点在相应平面上的法向应力和剪应力。
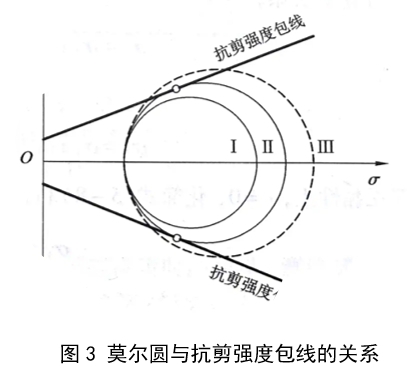
为判别M点岩石是否被破坏,可将该点的摩尔-应力圆与岩石的抗剪强度包线 绘在同一坐标图上并作相对位置比较。如图3所下,它们之间的关系存在以下三种情况:
(1)M点摩尔-应力图整体位于抗剪强度包线的下方(圆1),摩尔-应力圆与抗剪强度线相离,表明该点在任何平面上的剪应力均小于抗剪强度,表明该点未被剪破。
(2)M点摩尔-应力圆与抗剪强度包线相切(圆2),说明在切点所代表的平面上,剪应力恰好等于抗剪强度,该点就处于极限平衡状态,此时摩尔-应力圆亦称极限应力圆,由图中切点的位置还可确定M点破坏面的方向。连接切点与摩尔-应力圆圆心,连线与横坐标之间的夹角为2αf,根据莫尔圆原理,可知土体中M点的破坏面与最大主应力α1作用面方向夹角为αf[图4(a)]。
(3)M点摩尔-应力圆与抗剪强度包线相割(圆3),则M点早已破坏,应力已超出弹性范畴,圆3所代表的应力状态是不可能存在的。
处于极限平衡状态时,从图4(a)中莫尔圆与抗剪σ3强度包线的几何关系可推得极限平衡条件为