初等函数
初等函数
一、定义
初等函数是由基本初等函数经过有限次的四则运算(加、减、乘、除)和复合运算所构成的函数类。
二、基本初等函数
(一)常数函数
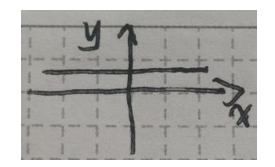
• 定义:形如y=C(C为常数)的函数,无论x取何值,对应的函数值都是常数C。
• 图像:在平面直角坐标系中,常数函数的图像是平行于 x 轴的直线。
(二)幂函数
• 定义:形如y=x^a(a为常数)的函数。其中,x是自变量,a是指数。
• 图像:幂函数的图像因指数a的不同而有较大差异。例如,当a=1时,图像是一条过原点且斜率为 1 的直线;当a=2时,图像是开口向上的抛物线。
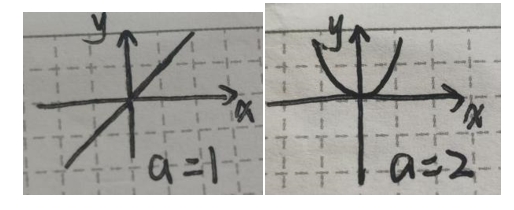
(三)指数函数
• 定义:形如y=a^x(a>0且a≠1)的函数。其中,a是底数,x是指数。
• 图像:指数函数的图像恒过点(0,1),当底数a>1时,函数单调递增;当底数0
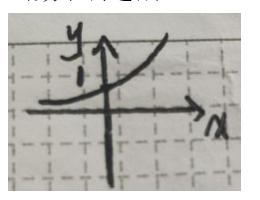
(四)对数函数
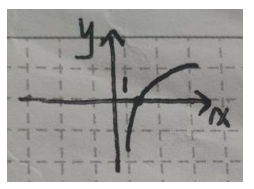
• 定义:形如y=log_a x(a>0且a≠1)的函数。其中,a是底数,x是真数。
• 图像:对数函数的图像恒过点(1,0),当底数a>1时,函数单调递增;当底数0
(五)三角函数
• 正弦函数:y=sinx,图像为波浪形曲线,周期为2Π,在[-1,1]之间波动。
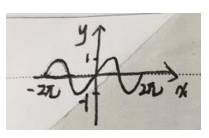
• 余弦函数:y=cosx,图像与正弦函数图像形状相同,只是在 x 轴上的位置有所不同,周期也是2Π。
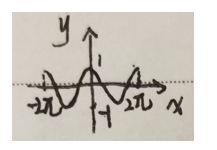
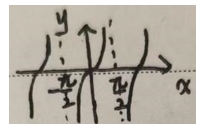
•正切函数:y=tanx,图像由无数支曲线组成,分别位于[-Π/2+kΠ,Π/2+kΠ],(k为整数)区间内,且关于原点对称。
(六)反三角函数
• 反正弦函数:y=arcsinx,定义域为[-1,1],值域为[-Π/2,Π/2],图像是正弦曲线在[-Π/2,Π/2]上的反函数图像。
• 反余弦函数:y=arccosx,定义域为[-1,1],值域为[0,Π],图像是余弦曲线在[0,Π]上的反函数图像。
• 反正切函数:y=arctanx,定义域为全体实数,值域为(-Π/2,Π/2),图像是正切曲线在(-Π/2,Π/2)上的反函数图像。
三、初等函数的形成
(一)四则运算
• 加法:两个函数f(x)和g(x)相加,得到新的函数h(x)=f(x)+g(x)。
• 减法:两个函数f(x)和g(x)相减,得到新的函数h(x)=f(x)-g(x)。
• 乘法:两个函数f(x)和g(x)相乘,得到新的函数h(x)=f(x)g(x)。
• 除法:两个函数f(x)和g(x)相除,得到新的函数h(x)=f(x)/g(x),其中g(x)≠0。
(二)复合运算
• 复合函数:设函数y=f(u),而u又是x的函数,即u=g(x),并且g(x)的值域与f(u)的定义域的交集非空,则y可以表示为x的函数,记作y=fg(x),这样的函数称为复合函数。
三、初等函数示例
• 多项式函数:形如y=a_n x^n+a{n-1}x^{n-1}+...+a_1 x+a_0,由常数函数和幂函数经过加法和乘法运算得到。
• 有理函数:形如y=P(x)/Q(x),其中P(x)和Q(x)都是多项式函数,由多项式函数经过除法运算得到。
• 指数复合函数:形如y=a^g(x),由指数函数和另一个函数g(x)复合而成。
• 对数复合函数:形如y=log_a g(x),由对数函数和另一个函数g(x)复合而成。
• 三角复合函数:例如y=sin(g(x)),由三角函数和另一个函数g(x)复合而成。
初等函数在数学、物理、工程等众多领域都有广泛的应用,是研究其他复杂函数的基础。
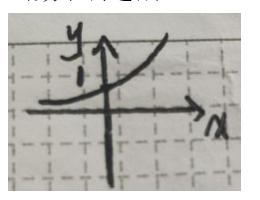
(四)对数函数
• 定义:形如y=log_a x(a>0且a≠1)的函数。其中,a是底数,x是真数。
• 图像:对数函数的图像恒过点(1,0),当底数a>1时,函数单调递增;当底数0

(五)三角函数
• 正弦函数:y=sinx,图像为波浪形曲线,周期为2Π,在[-1,1]之间波动。

• 余弦函数:y=cosx,图像与正弦函数图像形状相同,只是在 x 轴上的位置有所不同,周期也是2Π。

•正切函数:y=tanx,图像由无数支曲线组成,分别位于[-Π/2+kΠ,Π/2+kΠ],(k为整数)区间内,且关于原点对称。

(六)反三角函数
• 反正弦函数:y=arcsinx,定义域为[-1,1],值域为[-Π/2,Π/2],图像是正弦曲线在[-Π/2,Π/2]上的反函数图像。
• 反余弦函数:y=arccosx,定义域为[-1,1],值域为[0,Π],图像是余弦曲线在[0,Π]上的反函数图像。
• 反正切函数:y=arctanx,定义域为全体实数,值域为(-Π/2,Π/2),图像是正切曲线在(-Π/2,Π/2)上的反函数图像。
三、初等函数的形成
(一)四则运算
• 加法:两个函数f(x)和g(x)相加,得到新的函数h(x)=f(x)+g(x)。
• 减法:两个函数f(x)和g(x)相减,得到新的函数h(x)=f(x)-g(x)。
• 乘法:两个函数f(x)和g(x)相乘,得到新的函数h(x)=f(x)g(x)。
• 除法:两个函数f(x)和g(x)相除,得到新的函数h(x)=f(x)/g(x),其中g(x)≠0。
(二)复合运算
• 复合函数:设函数y=f(u),而u又是x的函数,即u=g(x),并且g(x)的值域与f(u)的定义域的交集非空,则y可以表示为x的函数,记作y=fg(x),这样的函数称为复合函数。
三、初等函数示例
• 多项式函数:形如y=a_n x^n+a{n-1}x^{n-1}+...+a_1 x+a_0,由常数函数和幂函数经过加法和乘法运算得到。
• 有理函数:形如y=P(x)/Q(x),其中P(x)和Q(x)都是多项式函数,由多项式函数经过除法运算得到。
• 指数复合函数:形如y=a^g(x),由指数函数和另一个函数g(x)复合而成。
• 对数复合函数:形如y=log_a g(x),由对数函数和另一个函数g(x)复合而成。
• 三角复合函数:例如y=sin(g(x)),由三角函数和另一个函数g(x)复合而成。
初等函数在数学、物理、工程等众多领域都有广泛的应用,是研究其他复杂函数的基础。

(五)三角函数
• 正弦函数:y=sinx,图像为波浪形曲线,周期为2Π,在[-1,1]之间波动。

• 余弦函数:y=cosx,图像与正弦函数图像形状相同,只是在 x 轴上的位置有所不同,周期也是2Π。

•正切函数:y=tanx,图像由无数支曲线组成,分别位于[-Π/2+kΠ,Π/2+kΠ],(k为整数)区间内,且关于原点对称。
