函数的特性

1.有界性

设函数f(x)在某区间I上有定义，若存在正数M（∃M＞0），使得∀x∈I，｜f(x)｜≤都成立，则称f(x)在I上有界.若这样的M不存在（即对充分大的M＞0都存在x∈I，使｜f(x)｜＞M），则称f(x)在I上无界.

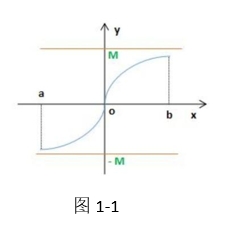
Tips:①函数有界等价于既有上界又有下界.（如图1-1）

(设函数f(x)的定义域为D，数集X∈D，如果存在数K₁ 使得f(x)≤K₁，对任一x∈X都成立那么称函数f(x)在X上有上界.下界同理.)

②讨论函数是否有界，必须指明定义域.

2. 奇偶性（定义域关于原点对称）

设函数f(x)的定义域D关于原点对称，若∀x∈D，有f(x)=f(-x)，则称f(x)为偶函数；若∀x∈D，有f(x)=-f(x)，则称f(x)为奇函数.

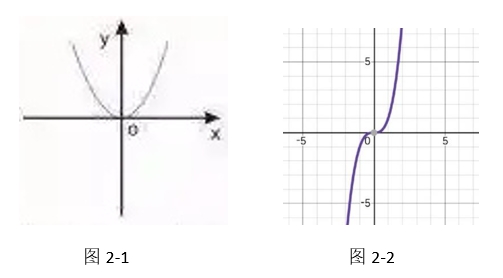
例如，f(x)=x²是偶函数（如图2-1），f(x)=x³为奇函数.（如图2-2）

3.单调性

设函数y=f(x)，x∈D.对任意的x₁、x₂∈I，则有x₁＜x₂，有f(x₁)＜f(x₂)，则称y=f(x)在I上单调递增；如有f(x₁)＞f(x₂) 则称y=f(x)在I上单调递减.

函数f(x)=x²在区间(0，+∞)上单调递增，在区间(-∞，0)上单调递减.（图2-1）

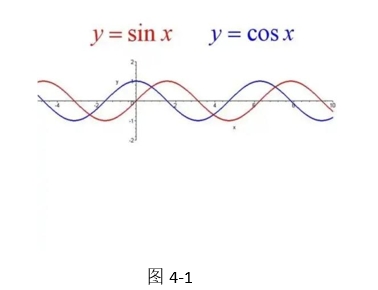
4.周期性

设函数y=f(x)，x∈D.如存在实数L≠0，使得f(x+L)=f(x)（x，x+L∈D），则称f(x)为周期函数，L为周期.一般地，周期函数的周期是指最小正周期.（如图4-1所示，y=sinx和y=cosx的周期为2π.）