反函数

一．反函数的定义

设函数f(x),x∈D的值域为C,若对于值域C中的每一个y，在D中有且仅有一个x使得x＝f-1（y）。按此对应法则得到一个定义在D上的函数，该函数称为y＝f（x）的反函数，记为x=f-1(x），y∈C。

．反函数的性质

1.函数f(x)存在反函数的必要条件：原函数f(x)必须是一一对应的；

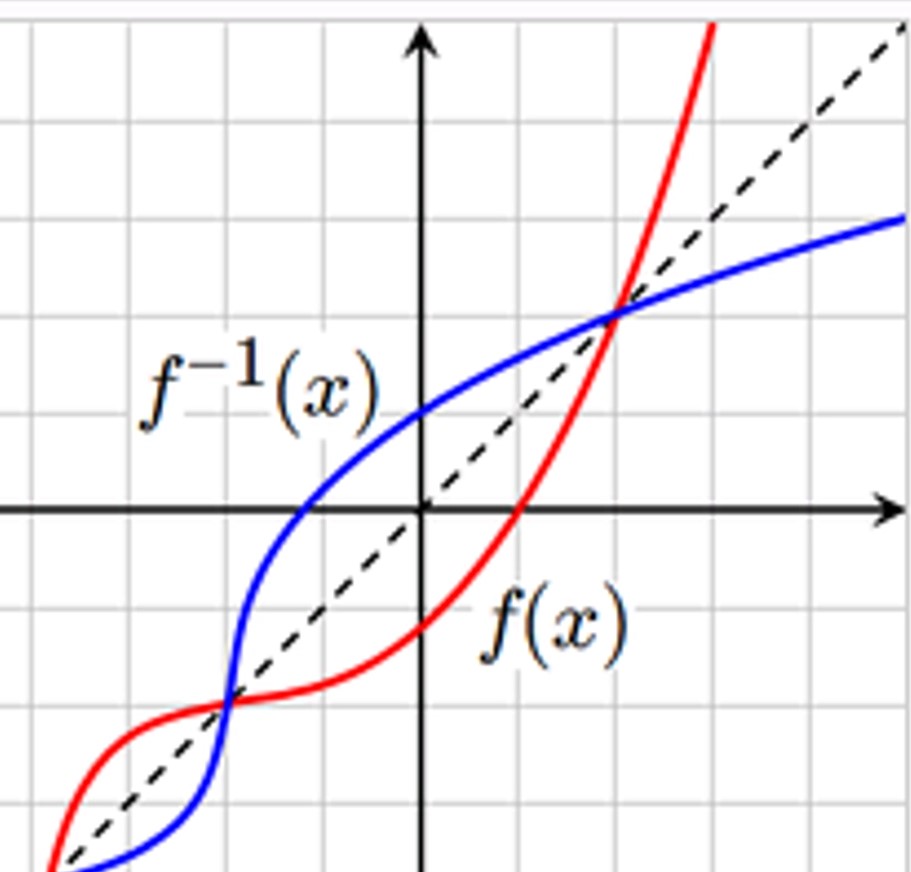
2.互为反函数的两个函数的图像，关于直线y=x对称；

3.一个函数与它的反函数在相应区间上单调性一致；

4.大部分偶函数不存在反函数，奇函数不一定存在反函数。若一个奇函数存在反函数，则它的反函数也是奇函数；

5.反函数是相互的，且具有唯一性；

6.互为相反数的两个函数定义域、值域相反，对应法则互逆；

7.严增（减）的函数，一定有严格增（减）的反函数。

三．如何求一个函数的反函数

1.反解出x；

2.互换x与y；

3.注明反函数定义域，即原函数值域。